本章主要是用Schrödinger方程来处理一维粒子的能量本征态问题,一般分为两类问题:
-
束缚态问题:束缚态(bound state)是指粒子局限在有限的空间中,即粒子在无穷远处出现的概率等于零的状态,即当 x→±∞ 时,有 ψ(x)→0 ;而非束缚态(或称散射态)指粒子可以出现在无穷远处的状态,即当 x→+∞ 或 x→−∞ 时, ψ(x)=0 。束缚态问题会给出势场函数 V(x) ,需要求出波函数 ψ(x) 以及能量本征值 E (通常是离散的 En )。
-
散射问题:会给出势场函数 V(x) 与能量 E ,需要求出波函数 ψ(x) 。
在求解上述两个问题的能量本征方程时,要根据具体物理问题的边界条件来定解。(束缚态问题还有着 limx→∞ ψ(x)=0 的无穷远处条件)
如果对一个给定的能量 E ,只有一个线性独立的波函数存在,则称该能级是非简并的;否则称它是简并的,其线性独立的波函数的个数称为它的简并度。
定义一维粒子的空间反射算符 P 为
Pψ(x)=ψ(−x)
其对应的本征方程为
Pψ(x)=πψ(x)
定义宇称(parity)为空间反射算符的本征值 π ,可以证明,空间反演算符只有 ±1 两个本征值,
Pψ(x)=ψ(−x)={ψ(x),−ψ(x),π=+1,π=−1,偶(正)宇称奇(负)宇称
即空间反射不变的波函数具有偶(正)宇称(even parity);变号的波函数具有奇(负)宇称(odd parity);还有一些波函数没有确定的宇称,它们不是空间反射算符的本征态。
质量为 m 的粒子,沿 x 方向运动,势能为 V(x) ,则定态Schrödinger方程表示为
[−2mℏ2dx2d2+V(x)]ψ(x)=Eψ(x)
在量子力学中,如果不作特别的声明,都认为 V(x) 取实值,即 V(x)=V∗(x) 。
设 ψ(x) 是定态Schrödinger方程的一个解,对应的能量本征值为 E ,则 ψ∗(x) 也是该方程的一个解,对应的能量也是 E 。
对定态Schrödinger方程取复共轭,可得
[−2mℏ2dx2d2+V(x)]ψ∗(x)=Eψ∗(x)
显然 ψ∗(x) 也是定态Schrödinger方程的解,且对应的能量本征值为 E 。
假设对应于能量的某个本征值 E ,定态Schrödinger方程的解无简并,则可取为实解(除了一个无关紧要的常数因子外)。
对应于能量的某个本征值 E ,总可以找到定态Schrödinger方程的一组实解,凡属于 E 的任何解,均可表示为这一组实解的线性叠加。
对于能级有简并的情况,要用到此定理;通过定理1和定理2,可以说明定态Schrödinger方程的基本解组可全取为实解。
假设 ψ(x) 是定态Schrödinger方程的一个解:
如果 ψ(x) 是实解,则可把它归入实解的集合中去;
如果 ψ(x) 是复解,则由定理1可知, ψ∗(x) 也是方程的解,且同属于能量本征值 E 。根据线性微分方程解的叠加性定理,
φ(x)=ψ(x)+ψ∗(x),χ(x)=−i[ψ(x)−ψ∗(x)]
也是方程同属于能量 E 的解,且彼此独立。 φ(x) 和 χ(x) 均为实解, 而 ψ(x) 和 ψ∗(x) 均可表示为其线性叠加,即
ψ=21(φ+iχ),ψ∗=21(φ−iχ)
设势能函数 V(x) 具有空间反射不变性,即 V(x)=V(−x),那么若 ψ(x) 是定态Schrödinger方程对应于能量本征值 E 的解,则 ψ(−x) 也是该方程对应于能量 E 的解。
当 x⟶−x 时,有
dx2d2⟶d(−x)2d2=dx2d2,V(x)⟶V(−x)=V(x)
则定态Schrödinger方程转化为
[−2mℏ2dx2d2+V(x)]ψ(−x)=Eψ(−x)
显然 ψ(−x) 也是定态Schrödinger方程的解,且对应的能量本征值为 E 。
如果对应于某能量 E ,定态Schrödinger方程的解无简并,则解必有确定的宇称。
因为此时 ψ(x) 与 ψ(−x) 代表同一个解,它们最多可以差一个常数因子 π ,即 Pψ(x)=ψ(−x)=πψ(x) 。
设势能函数 V(x) 具有空间反射不变性,即 V(x)=V(−x),则对应于任何一个能量本征值 E ,总可以找到定态Schrödinger方程的一组解 (每个解都有确定的宇称),而属于能量本征值 E 的任何解,都可用它们来展开.
对于能级有简并的情况,能量本征态并不一定就具有确定宇称,此时,可以用该定理来处理;通过定理3和定理4,可以说明定态Schrödinger方程的基本解组可全取为具有确定宇称的解。
假设 ψ(x) 是定态Schrödinger方程的一个解:
如果 ψ(x) 有确定的宇称,则可把它归入有确定的宇称的解集中去;
如果 ψ(x) 无确定的宇称,则由定理3可知, ψ(−x) 也是方程的解,且同属于能量本征值 E ,但不同于 ψ(x) 。根据线性微分方程解的叠加性定理,
f(x)=ψ(x)+ψ(−x),g(x)=ψ(x)−ψ(−x)
也是方程同属于能量 E 的解,且彼此独立。 f(x) 和 g(x) 均具有确定宇称: f(−x)=f(x) , g(−x)=−g(−x) ;而 ψ(x) 和 ψ(−x) 均可表示为其线性叠加,即
ψ(x)=21[f(x)+g(x)],ψ(−x)=21[f(x)−g(x)]
对于阶梯方位势
V(x)={V1,V2,x<ax>a
若 (V2−V1) 有限,则能量本征函数 ψ 及其导数 ψ′(x) 必定是连续的;但若 ∣V2−V1∣→∞ ,则该定理不成立。
根据定态Schrödinger方程
ψ′′(x)=−ℏ22m[E−V(x)]ψ(x)
在 V(x) 连续的区域,由 ψ′′(x) 存在可以推出 ψ(x) 与 ψ′(x) 是连续的。
在 V(x) 发生阶梯形跳跃处, V(x)ψ(x) 发生跃变,但变化是有限的,在 x∼a 邻域对上述方程积分,得
ε→0+lim∫a−εa+εψ′′(x)dx=ψ′(a+0+)−ψ′(a−0+)=−ℏ22mε→0+lim∫a−εa+εdx[E−V(x)]ψ(x)
由于 [E−V(x)]ψ(x) 是有限的,当 ε→0+ 时,上式右边积分趋于零,因此
ψ′(a+0+)=ψ′(a−0+)
即 ψ′(x) 在 V(x) 的跳跃点 x=a 处是连续的,因而 ψ(x) 也是连续的。
若 ψ1(x) 与 ψ2(x) 均为定态Schrödinger方程属于同一能量 E 的解,则
ψ1ψ2′−ψ2ψ1′=Const(与x无关)
其中 ψ1ψ2′−ψ2ψ1′ 称为 ψ1(x) 与 ψ2(x) 的Wronskian行列式,即
W[ψ1,ψ2](x)=ψ1(x)ψ1′(x)ψ2(x)ψ2′(x)
由定态Schrödinger方程可得
ψ1′′=−ℏ22m[E−V(x)]ψ1ψ2′′=−ℏ22m[E−V(x)]ψ2
ψ1 × 下式 − ψ2 × 上式,可得
ψ1ψ2′′−ψ2ψ1′′=0
即
ψ1ψ2′′−ψ2ψ1′′=ψ1ψ2′′+ψ1′ψ2′−ψ1′ψ2′−ψ2ψ1′′=(ψ1ψ2′−ψ2ψ1)′=0
积分,得
ψ1ψ2′−ψ2ψ1′=Const(与x无关)
对于束缚态,当 x→∞ 时, ψ→0 ,所以该定理中的常数必为 0 ,因此对于同属于能量 E 的任何两个束缚态波函数 ψ1 与 ψ2 ,
ψ1ψ2′=ψ2ψ1′
设粒子在规则势场 V(x) (无奇点)中运动,如存在束缚态,则必定是非简并的。
注:对于常见的不规则势阱,在绝大多数情况下(如无限深方势阱、 δ 势阱等),该定理也成立;但对于某些不规则势阱,如一维氢原子( V(x)∝−∣x∣1),除基态外,其他束缚态简并度均为 2 ,其特征是波函数的节点(指 ψ(x)=0 的点)出现在 V(x) 的奇异点处,两个简并态具有不同宇称。
设 ψ1 与 ψ2 是定态Schrödinger方程属于同一能量 E 的两个束缚态解,则
ψ1ψ2′=ψ2ψ1′
在不包含 ψ1(x) 和 ψ2(x) 节点的区域中,等式左右两边同除以 ψ1ψ2 ,得
ψ2ψ2′=ψ1ψ1′
即
(lnψ2ψ1)′=0
积分得
lnψ2ψ1=lnC(C是与x无关的常数)
故
ψ1=Cψ2
这表明 ψ1 与 ψ2 代表同一个量子态,即能级不简并。
一维无限深方势阱表示为
V(x)={0,∞,0<x<a0<x,x>a
在该势阱中的质量为 m 的粒子,能量是量子化的,即构成的能谱是离散的,体系的能量本征值
En=2ma2ℏ2π2n2(n=1,2,3,⋯)
对应的能量本征函数为
ψn(x)={a2sin(anπx),0,0<x<ax<0,x>a
注:若将一维无限深方势阱表示为
V(x)={0,∞,∣x∣<2a∣x∣>2a
则能量本征值不变,能量本征函数变为
ψn(x)=⎩⎨⎧{2acos(anπx),2asin(anπx),n=1,3,5,⋯,(偶宇称)n=2,4,6,⋯,(奇宇称)0,∣x∣<2a∣x∣<2a
在势阱内 (0<x<a) ,能量本征方程为
dx2d2ψ(x)+ℏ22mEψ(x)=0
其中粒子的能量 E>0 ,令
k=ℏ2mE>0
则能量本征方程可表示为
dx2d2ψ(x)+k2ψ(x)=0
解得
ψ(x)=Asin(kx+δ)
其中 A 与 δ 为待定常数。因为势壁无限高,从物理上考虑,粒子不能透过势壁;按波函数的统计诠释,要求在阱壁上及阱外波函数为 0 。这样就得到了边界条件
ψ(0)=0,ψ(a)=0
由 ψ(0)=Asin(δ)=0 ,可取 δ=0 ,则 ψ(x)=Asin(kx) ,由 ψ(a)=Asin(ka)=0 ,可知
ka=nπ⟹k=anπ(n=1,2,3,⋯)
注: n=0 给出的波函数 ψ(x)=0 ,无物理意义;而 n 取负值与 n 取对应的正值得到的波函数只相差一个常数 −1 ,描述的是同一个量子态。
k=ℏ2mE=anπ⟹En=2ma2ℏ2π2n2(n=1,2,3,⋯)
则能量本征函数
ψn(x)=Asin(anπx)
归一化后可得
ψn(x)=a2sin(anπx)
En=2ma2ℏ2π2n2∝n2(n=1,2,3,⋯)
能级的分布是不均匀的,能级越高,密度越小
ΔEn≈ma2ℏ2π2n,EnΔEn=n2⟶n→∞0
当 n 充分大时,可以认为能量连续。
最低能级不为零:
E1=2ma2ℏ2π2>0
这可以用不确定性关系来解释:
粒子局限在无限深方势阱中,位置不确定度 Δx∼a ,则动量不确定度 Δp∼Δxℏ∼aℏ ,故能量不能为零,
E∼2mp2∼2m(Δp)2∼2ma2ℏ2=0
ρn(x)=∣ψn(x)∣2=a2sin2(anπx)
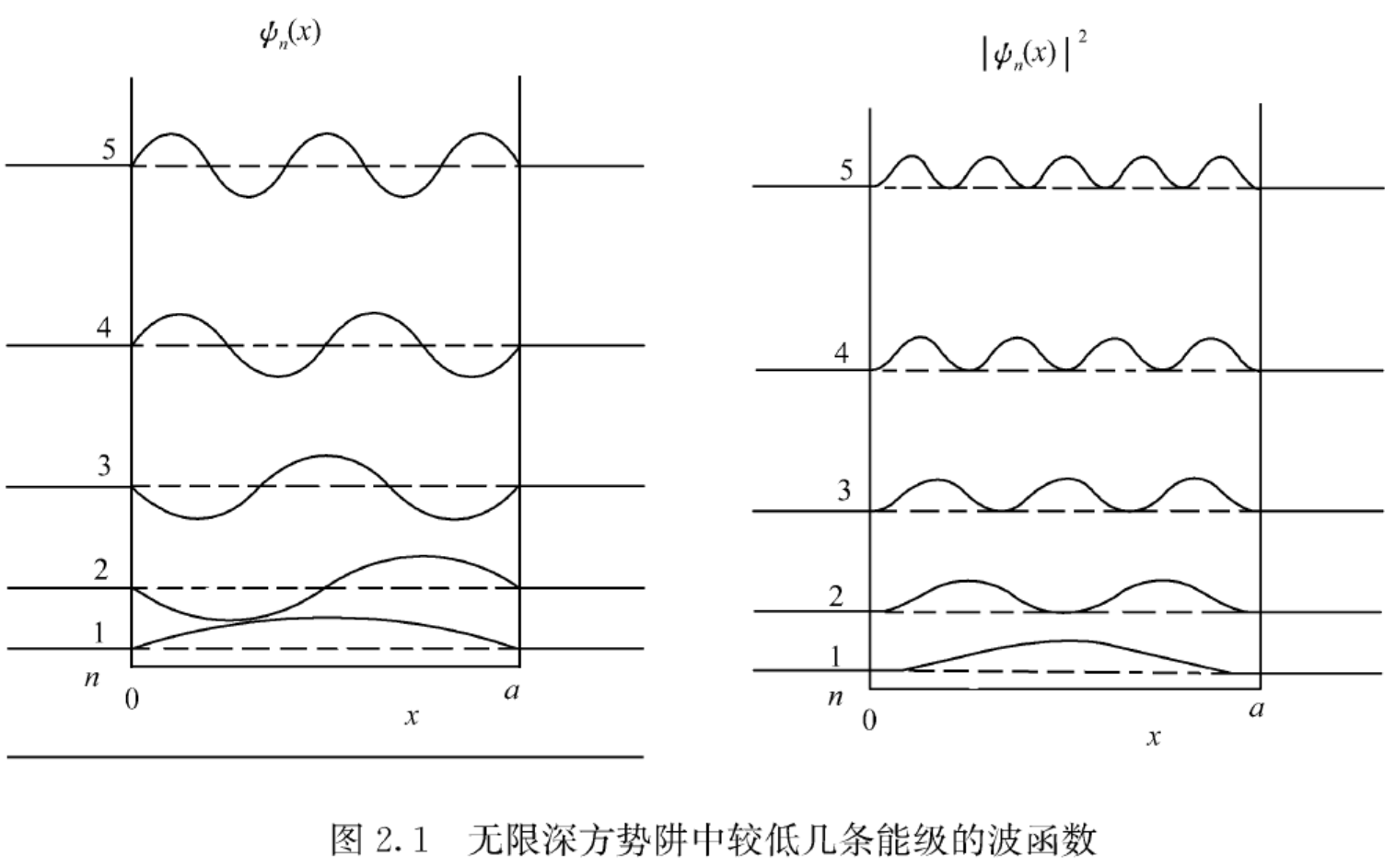
由该图也可以看出,除端点 (x=0,a) 外,基态(能量最低态, n=1 )波函数无节点,第 k 激发态( k=n−1 )有 k 个节点。
一维有限深对称方势阱表示为
V(x)={0,V0,∣x∣<2a∣x∣>2a
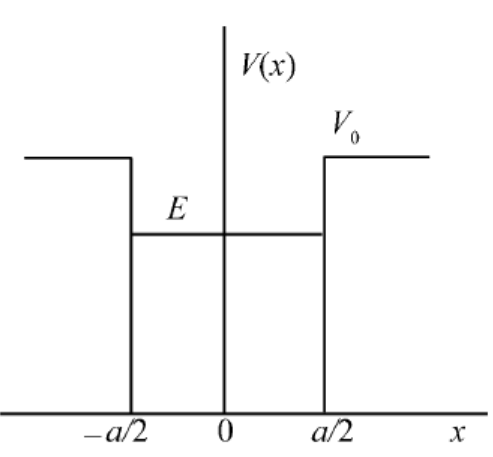
在该势阱中的质量为 m 的粒子,讨论其处于束缚态 (0<E<V0) 的情况。
令
k=ℏ2mE ,β=ℏ2m(V0−E)
引入无量纲参数
ξ=2ka ,η=2βa
这两个无量纲参数满足一定的方程组,使得其取值是离散的,对应的能量本征态为
En=ma22ℏ2ξn2
对于偶宇称态:
波函数形式为(可利用波函数连续性与归一化进一步求出 A 与 C )
ψ(x)=⎩⎨⎧Ceβx,Acos(kx),Ce−βx,x<−2a−2a<x<2ax>2a
无量纲参数满足方程组
{ξtanξ=ηξ2+η2=2ℏ2mV0a2
对于奇宇称态:
波函数形式为(可利用波函数连续性与归一化进一步求出 B 与 C )
ψ(x)=⎩⎨⎧Ceβx,Bsin(kx),−Ce−βx,x<−2a−2a<x<2ax>2a
无量纲参数满足方程组
{−ξcotξ=ηξ2+η2=2ℏ2mV0a2
先考虑势阱外的情况,能量本征方程为
dx2d2ψ(x)−β2ψ(x)=0
其中 β=ℏ2m(V0−E) ,解得
ψ(x)=Ceβx+De−βx
考虑束缚态边界条件,即在 x→∞ 处,要求 ψ(x)→0 ,则
ψ(x)={Ceβx,De−βx,x<−2ax>2a
再考虑势阱内的情况,能量本征方程为
dx2d2ψ(x)+k2ψ(x)=0
其中 k=ℏ2mE ,解得
ψ(x)=Acos(kx)+Bsin(kx)
考虑到势阱具有空间反射不变性 V(−x)=V(x) ,由定理3推论可知,束缚态能量本征函数(由定理7知其不简并)必具有确定的宇称,因此只能单独取 cos(kx) 或 sin(kx) 形式,以下分别讨论。
对于偶宇称态:
在势阱内 (∣x∣<2a) , B=0 ,
ψ(x)=Acos(kx)
在势阱外 (∣x∣>2a) , C=D ,
ψ(x)={Ceβx,Ce−βx,x<−2ax>2a
由定理5可知,波函数 ψ(x) 及导数 ψ′(x) 在 ∣x∣=2a 处是连续的,由于波函数具有偶宇称,在 −2a 与 2a 处的情况实际上是等效的,这里只用分析 x=2a 的情况。
ψ(x)={Acos(kx),Ce−βx,−2a<x<2ax>2aψ′(x)={−Aksin(kx),−Cβe−βx,−2a<x<2ax>2a
则
Acos(k2a)=Ce−β2a−Aksin(k2a)=−Cβe−β2a
两式相除,可消去 A,C ,得
ktan(k2a)=β
注:也可以直接考虑 (lnψ)′ 的连续性,从而直接消去 A,C 这两个常数。
引入无量纲参数
ξ=2ka ,η=2βa
可得
ξtanξ=η
同时, ξ 与 η 还满足
ξ2+η2=4a2(k2+β2)=4a2[ℏ22mE+ℏ22m(V0−E)]=2ℏ2mV0a2
整理即得 ξ 与 η 满足方程组
{ξtanξ=ηξ2+η2=2ℏ2mV0a2
对于奇宇称态:
在势阱内 (∣x∣<2a) , A=0 ,
ψ(x)=Bsin(kx)
在势阱外 (∣x∣>2a) , C=−D ,
ψ(x)={Ceβx,−Ce−βx,x<−2ax>2a
波函数 ψ(x) 及导数 ψ′(x) 在 x=2a 处是连续的,
ψ(x)={Bsin(kx),−Ce−βx,−2a<x<2ax>2aψ′(x)={Bkcos(kx),Cβe−βx,−2a<x<2ax>2a
则
Bsin(k2a)=−Ce−β2aBkcos(k2a)=Cβe−β2a
两式相除,可消去 B,C ,得
−kcot(k2a)=β
引入无量纲参数
ξ=2ka ,η=2βa
可得
−ξcotξ=η
同时, ξ 与 η 还满足
ξ2+η2=2ℏ2mV0a2
整理即得 ξ 与 η 满足方程组
{−ξcotξ=ηξ2+η2=2ℏ2mV0a2
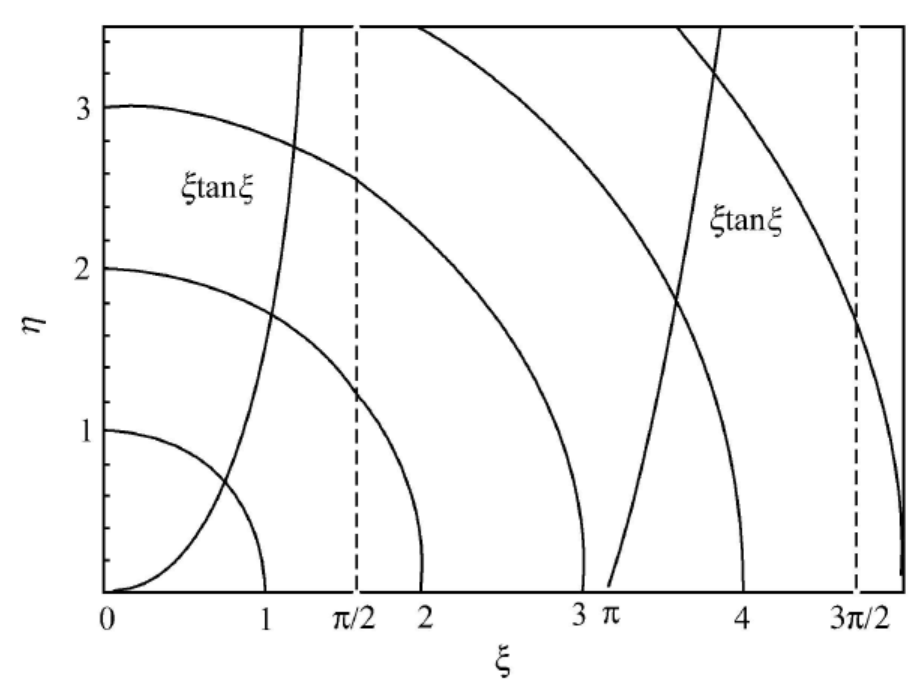
对于 ξ 与 η 满足的方程组,可以采用图解法近似求解,无论是奇宇称态还是偶宇称态,方程组中的第二个方程的图象都是圆弧,半径为 2ℏ2mV0a2 。对于偶宇称态,图为:
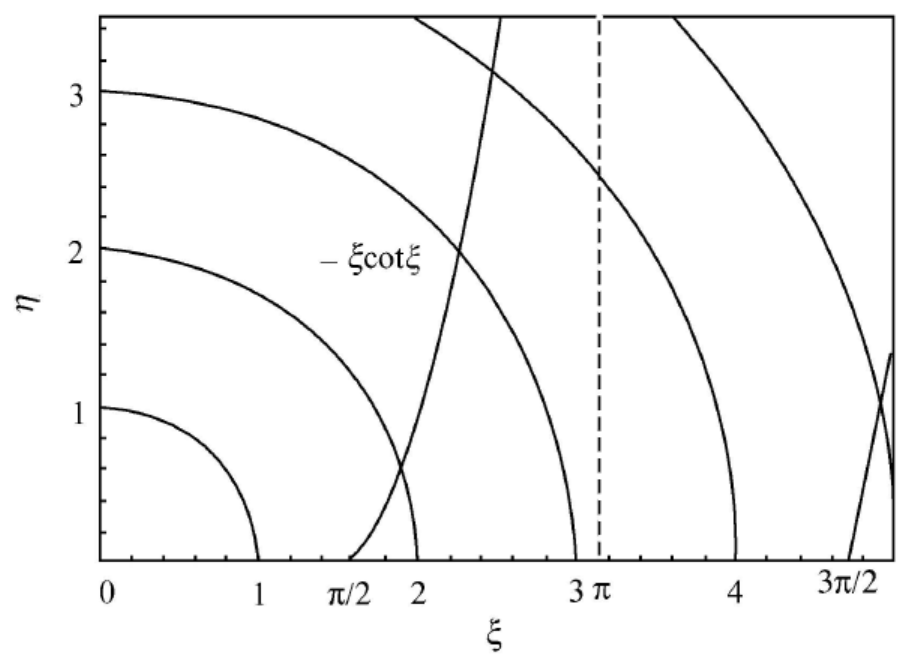
对于奇宇称态,图为:
注:实际上对于确定的 m,a,V0 ,图中的圆弧应该只有一条。
在一维有限深对称方势阱问题中,无论势阱多浅或多窄(即无论 V0a2 的值多小),偶宇称态的方程组都至少有一个根,这表明至少存在一个束缚态(即基态),其宇称为偶。
而对于奇宇称态的方程组,只有当
ξ2+η2=2ℏ2mV0a2≥(2π)2
即
V0a2≥2mπ2ℏ2
方程组才会有解,即才可能出现最低的奇宇称能级。
随着 V0a2 的增大,方程组的解的个数会逐渐增多,出现更高的激发态能级,宇称奇偶相间。由图可得,圆弧的半径 2ℏ2mV0a2 每增大 2π ,两图中交点的总个数会增加一个,由此可以推得束缚态能级总数为
N=1+⌊ℏπa2mV0⌋
ξ=2ka=2aℏ2mE⟹En=ma22ℏ2ξn2
由上图可得
0<ξ1<2π<ξ2<π<⋯<2π(n−1)<ξn<2πn<⋯
故有限深方势阱每个能级都比无限深方势阱的相应能级低一些:
En=ma22ℏ2ξn2<2ma2π2ℏ2n2
当 V0→+∞ 时,有 ξn→2πn ,则 En→2ma2π2ℏ2n2 ,即趋向于无限深方势阱的能级。
取谐振子的平衡位置为坐标原点,并选原点为势能的零点,则以为谐振子的势能可以表示为
V(x)=21mω2x2
其中 m 为谐振子的质量, ω 为经典谐振子的自然频率。理想的谐振子势是一个无限深势阱,只存在束缚态,谐振子的能量本征值为
En=(n+21)ℏω(n=0,1,2,⋯)
正交归一化的能量本征函数为
ψn(x)=Ane−2α2x2Hn(αx)
其中 α=ℏmω , Hn(x) 为Hermite多项式,归一化系数为
An=π2n⋅n!α
一维谐振子的能量本征方程为
[−2mℏ2dx2d2+21mω2x2]ψ(x)=Eψ(x)
令 α=ℏmω ,并引进无量纲参量
ξ=αx,λ=21ℏωE
则方程可整理为
dξ2d2ψ+(λ−ξ2)ψ=0
设解的形式为
ψ=e−2ξ2u(ξ)
之所以这么设,可以按如下方式考虑:当 ξ→∞ 时,方程近似表示为 dξ2d2ψ−ξ2ψ=0 ,当 ψ=e±2ξ2 时, ψ′=±ξe±2ξ2 , ψ′′=(ξ2±1)e±2ξ2≈ξ2e±2ξ2=ξ2ψ ,故方程的近似解为 ψ∼e±2ξ2 ,而根据束缚态边界条件,即 ξ→∞ 时 ψ→0 ,应舍去 ψ∼e2ξ2 。
将上述解的形式代入原方程,可得到 u(ξ) 满足的方程
dξ2d2u+2ξdξdu+(λ−1)u=0
此即Hermite方程,可以通过级数解法求解:在 ξ=0 附近,用幂级数展开
u(ξ)=k=0∑+∞ckξk
代入Hermite方程,比较同幂项的系数,可得
ck+2=(k+2)(k+1)2k−(λ−1)ck(k=0,1,2,⋯)
故所有的偶次项系数都可以用 c0 来表示,所有的奇次项系数都可以用 c1 来表示,把 c0 与 c1 作为两个任意常数,就可以得到Hermite方程两个线性无关的解,即级数的偶次项部分与奇次项部分
u1(ξ)=m=0∑+∞c2mξ2m=c0+c2ξ2+c4ξ4+⋯u2(ξ)=m=0∑+∞c2m+1ξ2m+1=c1ξ+c3ξ3+c5ξ5+⋯
考虑当 ξ→∞ 时的情况,当 k→+∞ 时,
ckck+2=(k+2)(k+1)2k−(λ−1)→k2
对于偶数的情况,即 k=2m ,有 c2m+2/c2m∼1/m ,这与 eξ2 的Taylor展开
eξ2=m=0∑+∞m!ξ2m
相邻两项的系数比相同,因此,
u1(ξ)∼eξ2
同理可得
u2(ξ)∼ξeξ2
代回到波函数可得
ψ1=e−2ξ2u1(ξ)∼e2ξ2ψ2=e−2ξ2u2(ξ)∼ξe2ξ2
这不满足束缚态的边界条件(当 ξ→∞ 时 ψ→0 ),故 u1 和 u2 两个无穷级数解中,必须至少有一个中断为多项式,也就是要找到合适的 λ ,使得存在 k∈N 满足 (k+2)(k+1)2k−(λ−1)=0 ,故当
λ−1=2n(n=0,1,2,⋯)
时,级数将中断一个多项式( cn+2=cn+4=cn+6=⋯=0 )。当 n 为偶时, u1 中断为Hermite多项式 Hn(ξ) ,u2 仍为无穷级数;当 n 为奇时, u2 中断为Hermite多项式 Hn(ξ) ,u1 仍为无穷级数。其中Hermite多项式表示为
Hn(ξ)=(−1)neξ2dξndne−ξ2=(2ξ)n+n(n−1)(2ξ)n−2+⋯+(−1)⌊2n⌋⌊2n⌋!n!(2ξ)n−2⌊2n⌋
例如
H0(ξ)=1H1(ξ)=2ξH2(ξ)=4ξ2−2
Hermite多项式的带权正交归一性表示为
∫−∞+∞Hm(ξ)Hn(ξ)e−ξ2dξ=π2n⋅n!δmn
根据 λ 满足的离散化条件,可以求出一维谐振子的能量本征值
λ=21ℏωE=2n+1⟹En=(n+21)ℏω(n=0,1,2,⋯)
借助Hermite多项式,并把 ξ=αx 代入,可以表示出一维谐振子的能量本征函数
ψn∝e−2ξ2Hn(ξ)⟹ψn(x)=Ane−2α2x2Hn(αx)
根据Hermite多项式的带权正交归一性,
(ψm,ψn)=AmAn∫−∞+∞Hm(ξ)Hn(ξ)e−ξ2dξ=AmAnπ2n⋅n!δmn
可得归一化系数
An=π2n⋅n!α
这样波函数就满足了正交归一化条件
(ψm,ψn)=δmn
En=(n+21)ℏω(n=0,1,2,⋯)
一维谐振子的能量是均匀分布的,相邻的两条能级间距为 En+1−En=ℏω 。
最低的三条能级上的谐振子波函数如下:
ψ0(x)=π41αe−2α2x2ψ1(x)=π412ααx e−2α2x2ψ2(x)=π4112α(2α2x2−1)e−2α2x2
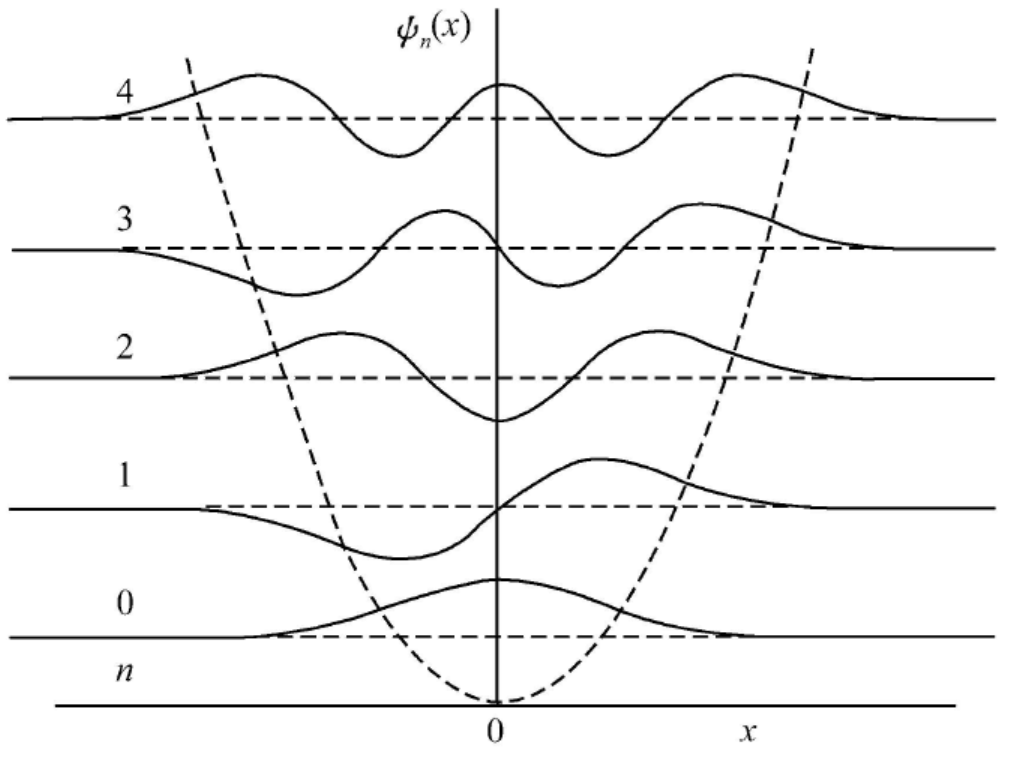
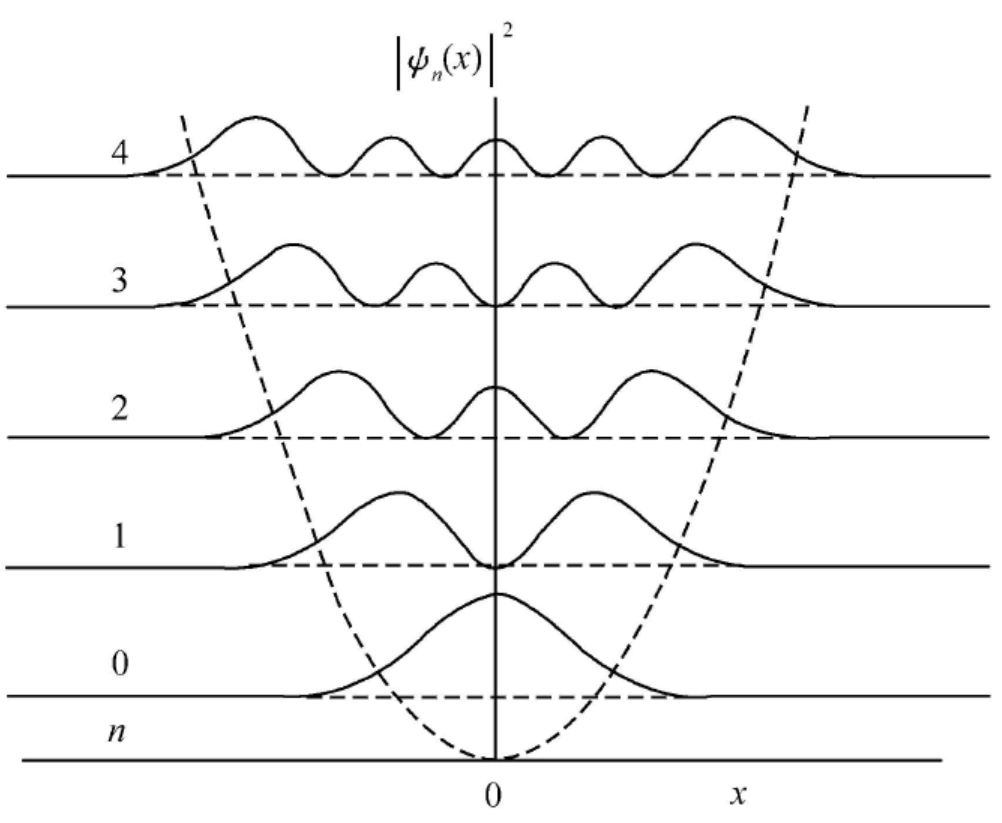
其中 ψn(x) 有 n 个节点。
由于一维谐振子势具有空间反射不变性( V(−x)=V(x) ),根据定理3推论, ψn(x) 必有确定的宇称,事实上,可以证明
ψn(−x)=(−1)nψn(x)
能级的宇称偶奇相间,基态是偶宇称。
一维谐振子基态能量为
E0=21ℏω
其并不为零(可以用不确定性关系解释),称为零点能。
处于基态的谐振子在空间的概率分布为
∣ψ0(x)∣2=παe−α2x2
这是一个Gauss型分布,在原点 (x=0) 处找到粒子的概率最大。
对于一维谐振子,其Hamilton算符
H^=−2mℏ2∂x2∂2+21mω2x2
二维谐振子的势能可以表示为
V(x,y)=21mω2r2=21mω2(x2+y2)
其Hamilton算符可以表示为
H^=−2mℏ2(∂x2∂2+∂y2∂2)+21mω2(x2+y2)=H^x+H^y
对于二维谐振子的能量本征方程
H^ψ(x,y)=Eψ(x,y)
由于 x,y 相独立,可以使用分离变量法求解,令 ψ(x,y)=ψx(x)ψy(y) ,则能量本征方程可表示为
(H^x+H^y)ψxψy=Eψxψy⇓ψyH^xψx+ψxH^yψy=Eψxψy⇓ψxH^xψx+ψyH^yψy=E
这样,能量本征方程就可以分离为 x,y 两个方向上的方程:
H^xψx=Exψx ,H^yψy=Eyψy
则二维谐振子的能量本征函数为
ψnxny(x,y)=ψnx(x)ψny(y)(nx,ny=0,1,2,⋯)
其中 ψnx,ψny 与一维谐振子的 ψn 函数相同。
二维谐振子的能量本征值为
Enxny=Enx+Eny=(21+nx)ℏω+(21+ny)ℏω=(1+nx+ny)ℏω(nx,ny=0,1,2,⋯)
其中 Enx,Eny 与一维谐振子的 En 表达式相同,记 N=nx+ny ,则
Enxny=(1+N)ℏω(N=0,1,2,⋯)
对于给定的 N , (nx,ny) 的可能取值共有 N+1 种(即 (0,N),(1,N−1),⋯,(N,0) ),故能级简并度
fN=N+1
三维谐振子的结论与二维谐振子类似,能量本征函数为
ψnxnyny(x,y,z)=ψnx(x)ψny(y)ψnz(z)(nx,ny,nz=0,1,2,⋯)
能量本征值为
Enxnyny=Enx+Eny+Enz=(21+nx)ℏω+(21+ny)ℏω+(21+nz)ℏω=(23+nx+ny+nz)ℏω(nx,ny,ny=0,1,2,⋯)
记 N=nx+ny+nz ,则
Enxnynz=(23+N)ℏω(N=0,1,2,⋯)
对于给定的 N , (nx,ny,nz) 的可能取值共有
nx=0∑N(N+1−nx)=k=1∑N+1k=21(N+1)(N+2)
故能级简并度
fN=21(N+1)(N+2)
δ 势阱表示为
V(x)=−γδ(x)(γ>0)
质量为 m 的粒子在 δ 势阱中运动:在 x=0 处有 V(x)=0 ,所以 E>0 为游离态, E 可以取一切正实数值,是连续变化的;而 E<0 时,则可能存在束缚能量本征态, E 只能取离散值。以下讨论束缚态,即 E<0 的情况。
能量本征方程为
ψ′′(x)=−ℏ22m[E+γδ(x)]ψ(x)
左右两边同时积分可以得到 δ 势阱中 ψ′ 的跃变条件:
ε→0+lim∫−εεψ′′(x)dx=ε→0+lim∫−εε−ℏ22m[E+γδ(x)]ψ(x)dx⇓ψ′(0+)−ψ′(0−)=−ℏ22mγψ(0)
令
β=ℏ−2mE>0
则在 x=0 的区域,能量本征方程可化为
ψ′′(x)−β2ψ(x)=0
解得
ψ(x)=Aeβx+Be−βx
考虑到束缚态边界条件,即在 x→∞ 处,要求 ψ(x)→0 ,则
ψ(x)={Aeβx,Be−βx,x<0x>0
考虑到势阱具有空间反射不变性 V(−x)=V(x) ,由定理3推论可知,束缚态能量本征函数(由定理7知其不简并)必具有确定的宇称,以下分别讨论:
对于偶宇称态:
波函数应表示为
ψ(x)={Aeβx,Ae−βx,x<0x>0
按照 ψ′ 跃变条件
ψ′(0+)−ψ′(0−)=−ℏ22mγψ(0)⇓−Aβ−Aβ=−ℏ22mγA
可得
β=ℏ2mγ
则可得出粒子的能量本征值
β=ℏ2mγ=ℏ−2mE⟹E=−2ℏ2mγ2
由归一化条件可得
(ψ,ψ)=2∫0+∞∣A∣2e−2βxdx=β∣A∣2=1
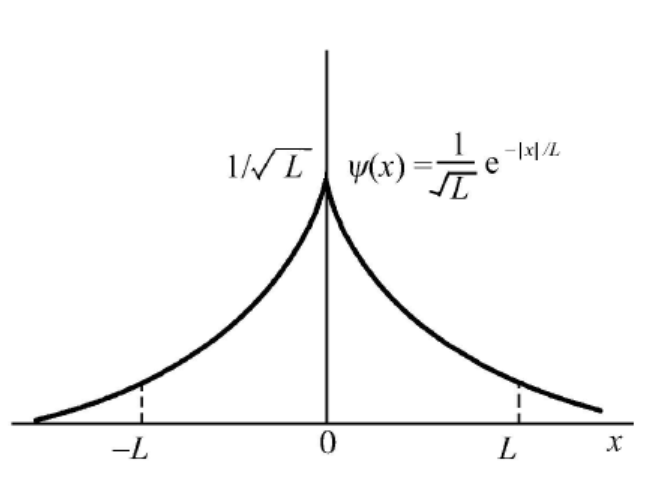
取 δ 势的特征长度
L=β1=mγℏ2
则
∣A∣=β=L1
这样归一化的束缚能量本征态波函数可表示为
ψ(x)=L1e−L∣x∣
对于奇宇称态:
波函数应表示为
ψ(x)={Aeβx,−Ae−βx,x<0x>0
由波函数在 x=0 点连续,可以得到
ψ(0−)=ψ(0+)⟹A=−A⟹A=0
所以不可能存在奇宇称束缚能量本征态。
从物理上考虑,奇宇称波函数在 x=0 点必为零,而 δ 势又恰好只在 x=0 点其作用,所以 δ 势阱对奇宇称态没有影响,因而不可能形成束缚态。
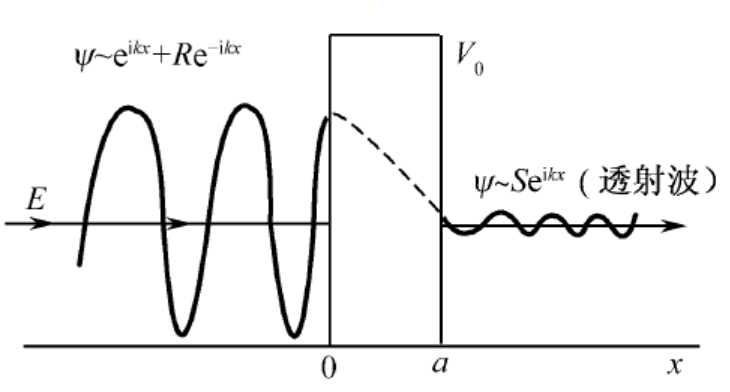
设具有一定能量 E 的质量为 m 的粒子沿 x 轴正方向射向方势垒
V(x)={V0 ,0 ,0<x<ax<0,x>a
无论粒子能量 E>V0 还是 E<V0 ,都有一定概率穿透势垒,也有一定概率被反射回去。主要考虑 0<E<V0 的情况,令
k=ℏ2mE,κ=ℏ2m(V0−E)
则波函数为
ψ(x)=⎩⎨⎧eikx+Re−ikx ,Aeκx+Be−κx ,Seikx ,x<00<x<ax>a
其中 Re−ikx 为反射波, Seikx 为透射波
透射系数为
T=∣S∣2=(k2+κ2)2sinh2(κa)+4k2κ24k2κ2=[1+V04E(1−V0E)1sinh2(κa)]−1
反射系数为
∣R∣2=(k2+κ2)2sinh2(κa)+4k2κ2(k2+κ2)2sinh2(κa)
在势垒外 (x<0,x>a) ,能量本征方程表示为
ψ′′(x)+ℏ22mEψ(x)=0
令 k=ℏ2mE ,该方程的两个线性无关解可取为 ψ(x)∼e±ikx 。粒子是从左入射,由于势垒的存在,在 x<a 的区域中,既有入射波 eikx ,也有反射波 e−ikx ;而在 x>a 的区域中,则只有透射波 eikx ,所以
ψ(x)={eikx+Re−ikx ,Seikx ,x<0x>a
这里把入射波的波幅任意地取为 1 ,只是为了方便求解,由于还没有归一化,只要相对比例一定,对透射和反射系数都没有影响。
在势垒内部 (0<x<a) ,能量本征方程表示为
ψ′′(x)−ℏ22m(V0−E)ψ(x)=0
令 κ=ℏ2m(V0−E) ,解得
ψ(x)=Aeκx+Be−κx(0<x<a)
根据 ψ 与 ψ′ 分别在 x=0 与 x=a 处连续,可以得到如下关于 R,S,A,B 的方程组
⎩⎨⎧1+R=A+Bik(1−R)=κ(A−B)Seika=Aeκa+Be−κaikSeikx=κ(Aeκa−Be−κa)
为了求解该方程组,可由前两个方程用 R 表示 A,B ,再由后两个方程用 S 表示 A,B ,两种表示对比可得到关于 S,R 的方程组,进一步求出 S 与 R ,回代得到 A,B ;或者使用线性代数的知识求解也可。完整的解较为复杂,这里不再展示。
入射的粒子流密度为
ji=−2miℏ(ψi∗dxdψi−ψidxdψi∗)=−2miℏ(e−ikxdxdeikx−eikxdxde−ikx)=mℏk=v
类似的,可以计算出反射流密度 jr 和透射流密度 jt 分别为
jr=−∣R∣2v,jt=∣S∣2v
所以
反射系数=∣ji∣∣jr∣=∣R∣2透射系数=∣ji∣∣jt∣=∣S∣2
代入求解方程组得到的 R,S ,得
透射系数为
T=∣S∣2=(k2+κ2)2sinh2(κa)+4k2κ24k2κ2
反射系数为
∣R∣2=(k2+κ2)2sinh2(κa)+4k2κ2(k2+κ2)2sinh2(κa)
∣R∣2+∣S∣2=1
通过整理,透射系数还可以表示为
T=[1+V04E(1−V0E)1sinh2(κa)]−1
当 0<E<V0 时,透射系数 T=0 ,这种粒子能穿透比它动能更高的势垒的现象,称为量子隧穿效应(或称隧道效应(tunnel effect)、势垒贯穿),它是粒子具有波动性的表现。当然,这种现象一般概率较低,只有在一定的条件下才比较显著。
设 κa≫1 ,则 sinh(κa)=21(eκa−e−κa)≈21eκa≫1 ,则透射系数可近似表示为
T≈(k2+κ2)2sinh2(κa)4k2κ2≈(k2+κ2)2(21eκa)24k2κ2=(k2+κ2)216k2κ2e−2κa=V0216E(V0−E)e−ℏ2a2m(V0−E)
若记
T0=16V0E(1−V0E)
则
T≈T0exp(−ℏ2a2m(V0−E))
可以看出 T 灵敏地依赖于粒子的质量 m 、势垒宽度 a 以及 (V0−E) 。
对于一般形状的势垒,可以将其视为许多方势垒相邻排布,若透射系数 T≪1 ,则对于在 a≤x≤b 之间的势垒,有 WKB准经典近似公式
T≈T0exp{−ℏ2∫ab2m[V(x)−E] dx}
首先考虑方势垒中 E>V0 的情况,令
k′=ℏ2m(E−V0)
只需要将 κ⟶ik′ ,可得透射系数
T=(k2−k′2)2sin2(k′a)+4k2k′24k2k′2=[1+41(k′k−kk′)2sin2(k′a)]−1
当 k′a=nπ 时, sin(k′a)=0 ,故 T=1 ,称为共振透射。
而对于方势阱的透射,上述理论仍然适用,只需要把 V0⟶−V0 ,则相应的
k′=ℏ2m(E+V0)≥ℏ2mE=k
此时透射系数
T=[1+41(k′k−kk′)2sin2(k′a)]−1=1+4V0E(1+V0E)sin2(k′a)−1
可以看出,若 V0=0 ,则 T=1 ;若 V0=0 ,则一般情况下 T<1,∣R∣2=0 ,即粒子有一定概率被势阱弹回。
对于给定势阱,透射系数 T 完全依赖于入射粒子的能量 E ,透射系数 T(E) 随 E 的变化如图所示
.png)
如果 E≪V0 ,则一般来说 T 值很小,除非入射粒子的能量 E 合适,使 sin(k′a)=0 ,此时 T=1 (反射系数 ∣R∣2=0 ),这种现象被称为共振透射,它出现的条件是
k′a=nπ(n=1,2,3,⋯)
可以得到共振能级 En 的表达式为
k′=ℏ2m(E+V0)=anπ⟹En=−V0+2ma2n2π2ℏ2
与此相对,反射最强的条件是
k′a=(n+21)π(n=0,1,2,⋯)
设具有一定能量 E 的质量为 m 的粒子沿 x 轴正方向射向 δ 势垒
V(x)=γδ(x)(γ>0)
能量本征方程为
ψ′′(x)=−ℏ22m[E−γδ(x)]ψ(x)
左右两边同时积分可以得到 δ 势阱中 ψ′ 的跃变条件:
ε→0+lim∫−εεψ′′(x)dx=ε→0+lim∫−εε−ℏ22m[E−γδ(x)]ψ(x)dx⇓ψ′(0+)−ψ′(0−)=ℏ22mγψ(0)
令
k=ℏ2mE>0
则在 x=0 的区域,能量本征方程可化为
ψ′′(x)+k2ψ(x)=0
该方程的两个线性无关解可取为 ψ(x)∼e±ikx 。粒子是从左入射,由于势垒的存在,在 x<0 的区域中,既有入射波 eikx ,也有反射波 e−ikx ;而在 x>0 的区域中,则只有透射波 eikx ,所以解得
ψ(x)={eikx+Re−ikx ,Seikx ,x<0x>0
根据在 x=0 处 ψ 连续与 ψ′ 的跃变条件,可以得到如下关于 R,S 的方程组
{1+R=SikS−ik(1−R)=ℏ22mγS
解得
S=1+ℏ2kimγ1R=1+ℏ2kimγ−ℏ2kimγ
则透射系数为
T=∣S∣2=1+ℏ4k2m2γ21=1+2ℏ2Emγ21
反射系数为
∣R∣2=1+ℏ4k2m2γ2ℏ4k2m2γ2=1+2ℏ2Emγ22ℏ2Emγ2
∣R∣2+∣S∣2=1
如果把 δ 势垒换为 δ 势阱( γ⟶−γ ),透射系数与反射系数的值均不变。
δ 势的特征长度 L=mγℏ2 ,特征能量为 ℏ2mγ2 。
透射波的波幅 S 只依赖于 ℏ2kmγ=k1/mγℏ2 ,即入射粒子波长与 δ 势特征长度之比;而透射系数 T 只依赖于 ℏ2Emγ2=ℏ2mγ2/E ,即特征能量与入射粒子能量之比。当 E≫ℏ2mγ2 时, T≈1 ,即高能极限下粒子将完全穿透 δ 势垒。








.png)